Modeling of Aerodynamic Forces in Flapping Flight with the Unsteady Vortex Lattice Method
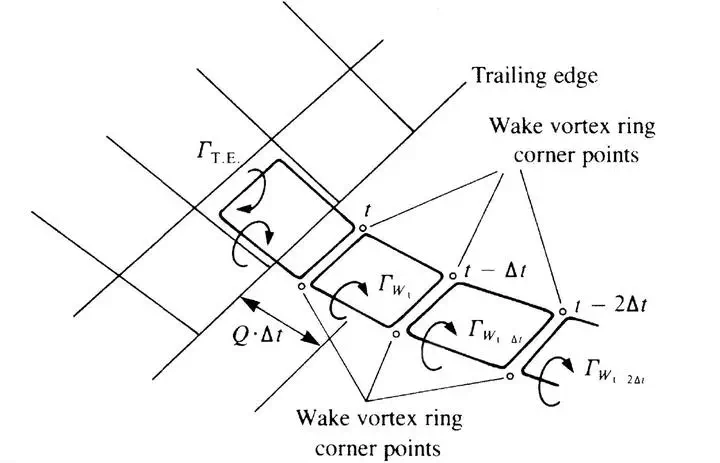 Katz & Plotkin, Low Speed Aerodynamics
Katz & Plotkin, Low Speed Aerodynamics
Abstract
This thesis concerns the extensive study and comparison of two approaches commonly used to compute the aerodynamic forces with the Unsteady Vortex Lattice Method. The first approach was introduced by Katz and Plotkin and is based on Bernoulli’s equations, the second approach was based Joukowski’s equations for the computation of forces.
The thesis is divided in two main sections: the study of one wing undergoing simple movements (steady, pure harmonic pitching and pure harmonic plunging) and the study of two separate wings undergoing a combination of flapping and pitching such as seen in avian flight.
For the simple test cases, the results obtained with both methods of computation were first compared to an analytical solution for a (quasi) 2D case. Then the comparison of both methods was made for finite wings. For the 3D problem a convergence study was done with respect to the chordwise discretisation of the airfoils. This section showed that for all the cases, the two methods give almost the same answer and therefore they could be considered as equivalent. The convergence study realised for finite wings showed however that Joukowski’s method converges quicker than Katz’s for symmetric airfoils, but it is the other way around when it comes to cambered airfoils.
The study of the flapping and pitching motion is based on the work of N. Abdul Razak. The influence of pitch leading was extensively studied as this phenomenon presents a flow attached at all time, so these kinematics are well suited for the Vortex Lattice Method. Both pure flapping and pitch lagging were also discussed but more briefly. For pitch leading, the study showed that in general both methods give the same results for the drag and the lift. Moreover, the UVLM solutions were very close to the experimental ones, especially for the drag. The convergence showed a small advantage for the Katz method for the coarser meshes, but in the end both methods appear to reach convergence for the same discretisation.
Additional info
This thesis was realized in completion of a Master’s degree in Aerospace Engineering at the University of Liège’s Aerospace and Mechanical Engineering Department. The grade of Cum Laude was obtained for this Master’s degree.
The most important findings were published in the AIAA Journal the following year.